实时基于FPGA的点云配准框架：超快且可配置的对应点搜索

邓岂，IEEE研究生会员，孙豪，IEEE会员，束宇豪，肖建中，姜伟雄，汪辉和Yajun Ha，IEEE高级会员

摘要

点云配准是基于LiDAR的定位与地图构建系统的关键组成部分，但现有的实现往往受限于有限的处理速度，在车载嵌入式CPU上仅能达到2 FPS，这主要是由于对应点搜索效率低下。为了解决这一挑战，我们提出了一种实时基于FPGA的点云配准框架，具有超快且可配置的对应点搜索能力。该框架包含三个关键创新：首先，我们开发了一种新颖的范围投影结构（RPS），将无序的LiDAR点组织成矩阵格式，以实现高效的点定位（points localization），并将邻近点分组到连续内存段中，从而加速点访问。其次，我们引入了一种高效的多模式对应点搜索算法，利用RPS结构有效地缩小搜索区域，消除冗余点，并通过利用LiDAR特有的激光通道信息支持各种类型的对应关系。第三，我们设计了一个可配置的超快速RPS基对应点搜索（RPS-CS）加速器，包括高性能的RPS构造器用于快速结构构建和高度并行的RPS搜索器用于快速对应点搜索，进一步通过动态缓存机制和流水线批处理单元来提高效率和可配置性。实验结果表明，RPS-CS加速器与最先进的FPGA实现相比实现了$7.5\times$$7.5 \times$倍的速度提升和$17.1\times$$17.1 \times$倍的能量效率改进，而所提出的框架实现了对64线激光雷达数据的实时性能，帧率为20.1 FPS。

关键词：FPGA，硬件加速，对应点搜索，点云配准，基于LiDAR的SLAM（LiDAR-based SLAM, LSLAM）

[^0]

I. 引言

点云配准是基于LiDAR的即时定位与地图构建（LSLAM）系统的关键组成部分，涉及计算一个变换矩阵以对齐源点云与目标点云，如图1所示。最先进的配准算法[1]的流程图如图2所示，它接收两种类型的特征点并计算最优变换矩阵。高效准确的配准实现一直是自动驾驶和机器人技术等领域的重要研究课题。

为了提高点云配准算法的准确性，需要采用具有更多激光通道和更高帧率的先进LiDAR系统。例如，3D LiDAR（Robosense Ruby Plus）已升级到128个激光器，扫描频率为20 Hz，每秒生成$4,608,000$$4,608,000$个点。然而，这种升级将不可避免地导致点云配准算法的执行时间大幅增加[2][3]。图3所示的性能剖析结果表明，即使使用来自64个激光器LiDAR的点云，点云配准算法[1]在车载嵌入式处理器（CPU）上也只能实现每秒不到2帧（FPS）的处理速度，这远不能满足实时需求。性能瓶颈在于对应搜索任务，该任务占整体配准时间的$91.6\mathrm{\%}$$91.6 \%$。

先前的研究通过优化搜索结构、搜索算法和专用硬件加速器，在点云配准中加速了对应搜索。一些研究[4]-[6]将稀疏且不均匀的点云组织成基于树或基于体素的搜索结构，从而实现了高效的K近邻对应（KNNC）搜索。然而，这些结构往往无法同时兼顾快速定位与提取邻近点，尤其是在高度不均匀的点分布下。此外，它们难以保留关键的三维结构和几何信息，限制了其处理几何对应如平面近邻（PNN-C）和边缘近邻（ENN-C）的能力。搜索算法也面临着实现并行性和高效处理几何对应方面的挑战。近似方法[7]-[10]减少了搜索时间，但牺牲了精度，而数据访问优化[11]、[12]如缓存和并行聚合提高了效率，但也增加了重新排序和调度的开销。

邓岂是中国科学院上海高等研究院；上海科技大学信息科学与技术学院；以及中国科学院大学。 孙豪隶属于东南大学电子科学与工程学院，南京 210096，中国。 束宇豪、肖建中和姜伟雄是上海科技大学信息科学与技术学院的成员，同时也在中国科学院上海微系统与信息技术研究所和中国科学院大学。 汪辉是中国科学院上海高等研究院微电子学院，北京 100045 的成员。电子邮件：[email protected] Yajun Ha 是上海科技大学信息科学与技术学院，中国；上海高效能和定制AI集成电路工程技术研究中心的成员。他是通讯作者。电子邮件：[email protected]

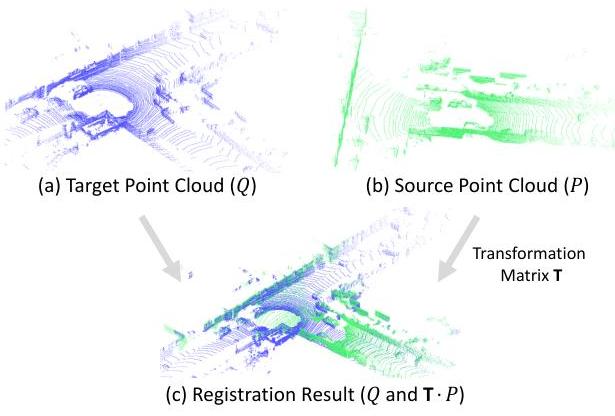
图 1. 点云配准算法示意图。

这些操作步骤限制了其实时应用性。硬件加速器，包括GPU和FPGA [13]-[15]，进一步提升了性能。GPU利用并行性来加速KD树构建和K近邻搜索，但能耗高，降低了能效。基于FPGA的解决方案 [5], [6] 更加节能，通过硬件与软件协同优化策略分配任务。然而，它们通常无法有效处理大规模数据的缓存存储与调度，或者为像PNN-C和ENN-C这样的多样化几何对应关系类型提供可配置支持，这对点云配准至关重要。

为了解决这个问题，我们提出了一种基于FPGA的实时LiDAR点云配准框架，配备了超快且可配置的对应关系搜索能力。我们做出了以下三个贡献。

• 一种新颖的搜索结构（RPS），用于高效的查询点定位和邻近点访问。RPS结构根据投影坐标和LiDAR的距离值将无序且分布不均的LiDAR点组织成类似矩阵的格式。为了便于快速访问邻近点，RPS将具有相似距离值和投影坐标的点分组到连续内存块中，显著降低了搜索复杂度。

• 利用RPS结构的高效多模式对应关系搜索算法。利用RPS提供的空间组织，所提出的算法有效地缩小了搜索区域并消除了大量冗余点。此外，通过结合特定于LiDAR的激光发射通道信息，该算法支持多模式对应关系搜索，实现了不同类型对应关系的快速准确搜索。

• 基于RPS的超快可配置化对应关系搜索加速器（RPS-CS）。RPS-CS框架包括两个关键组件：(1) RPSBuilder：一个高性能加速器，用于从LiDAR点云快速构建RPS结构数据。(2) RPS-Searcher：一个高度并行化且可配置化的加速器，用于快速对应关系搜索。为了提高内存访问效率，我们设计了一种动态RPS缓存机制，自适应预加载邻近点从外部内存到片上存储器。此外，为了增强搜索效率和可配置性，RPS-Searcher采用了流水线式批处理模块来将可变数量的点聚合为固定大小的批次。 本文其余部分的组织如下。第二节介绍了点云配准算法的背景知识及相关工作。第三节展示了所提框架的概述。第四节介绍了RPS结构及构建加速器。第五节展示了基于RPS的快速可扩展对应关系搜索算法及加速器。第六节给出了实验结果与分析。最后，第七节总结了结论和未来工作。

II. 背景与相关工作

A. 配准算法的定义与分析

在L-SLAM（激光同步定位与地图构建）系统的配准任务中，当前帧的点云被定义为源点云，记作P，并且前一帧的点云被定义为目标点云，记作Q，其中 $\mathrm{P},\mathrm{Q}\in {\mathbb{R}}^3$$\mathrm{P}, \mathrm{Q} \in \mathbb{R}^{3}$ 。通常情况下，一帧的点云指的是由LiDAR传感器在其360度水平旋转扫描过程中捕获的三维点云数据集。

点云配准的目标是通过变换矩阵 $T=(R,t)$$T=(R, t)$ 估计刚体运动参数，从而最大化变换后的源点云 $T\cdot P$$T \cdot P$ 和目标点云Q之间的重合度。这里，$R$$R$ 表示旋转矩阵，而 $t$$t$ 是平移向量。图1展示了配准算法。

图2给出了最先进的配准算法[1]的流程图，该算法接收两种类型的特征点并计算最优变换矩阵。在此背景下，与源点云中的平面和边缘相关的特征点分别标记为 $P_{\mathcal{H}}$$P_{\mathcal{H}}$ 和 $P_{\mathcal{E}}$$P_{\mathcal{E}}$ 。相应地，与目标点云中的平面和边缘相关的特征点分别表示为 $Q_{\mathcal{H}}$$Q_{\mathcal{H}}$ 和 $Q_{\mathcal{E}}$$Q_{\mathcal{E}}$ 。

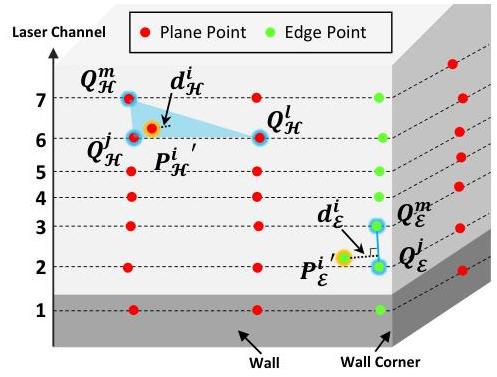
图4. 对应点搜索的示意图。带有蓝色圆圈的三个红色点构成了平面查询点 $P_{\mathcal{H}}^i{}^{\prime }$$P_{\mathcal{H}}^{i}{ }^{\prime}$ 的对应点。带有蓝色圆圈的两个绿色点构成了边缘查询点 $P_{\mathcal{E}}^{i^{\prime }}$$P_{\mathcal{E}}^{i^{\prime}}$ 的对应点。

通常情况下，如图4所示，平面点通常位于墙壁上，而边缘点则位于角落处。配准算法包含三个主要模块。

1. 构建搜索结构模块：第一模块专注于构建搜索结构，以高效地组织目标点云，以便后续模块能快速准确地进行对应点搜索。在SLAM算法中常用的搜索结构是K维树（KD树），这是一种空间划分技术，将点云组织成分层树格式，以便于快速搜索操作。因此，许多先前的工作，如[1]、[16]、[17]，采用KD树来构建 $Q_{\mathcal{H}}$$Q_{\mathcal{H}}$ 和 $Q_{\mathcal{E}}$$Q_{\mathcal{E}}$ 特征点的结构。我们用 $N_Q$$N_{Q}$ 表示用于构建搜索结构的目标点云中的点数。

2. 搜索对应模块：系统中的第二模块旨在建立源点云和目标点云之间的对应关系。对应的质量直接影响配准算法的准确性。利用前一模块开发的KD树搜索结构，[1]通过以下三个步骤搜索对应关系。

首先，使用初始的变换矩阵估计 $T_{\text{init }}=(R_{\text{init }},t_{\text{init }})$$T_{\text {init }}=\left(R_{\text {init }}, t_{\text {init }}\right)$ 将源点云中的点转换到目标点云的坐标系中，其中 $R_{\text{init }}$$R_{\text {init }}$ 和 $t_{\text{init }}$$t_{\text {init }}$ 分别表示旋转矩阵和平移向量。通过公式（1）分别转换为 $P_{\mathcal{H}}^{i^{\prime }}$$P_{\mathcal{H}}^{i^{\prime}}$ 和 $P_{\mathcal{E}}^{i^{\prime }}$$P_{\mathcal{E}}^{i^{\prime}}$ ，特征点 $P_{\mathcal{H}}^i$$P_{\mathcal{H}}^{i}$ 和 $P_{\mathcal{E}}^i$$P_{\mathcal{E}}^{i}$ 被转换后定义为查询点，查询点的数量记为 $N_P$$N_{P}$ 。

其次，搜索每个查询点的对应关系。如图2所示，对应关系可以分为三类：KNN-C、PNN-C和ENN-C。

1. KNN-C通常涉及识别K个最近邻作为每个查询点的对应点，这是基础功能，并在机器人应用中广泛使用。

2. PNN-C是指识别最近的三个平面特征点作为查询平面点的对应平面。在图4中，查询平面点$P_{\mathcal{H}}^{i^{\prime }}$$P_{\mathcal{H}}^{i^{\prime}}$的PNN-C点由$(Q_{\mathcal{H}}^j,Q_{\mathcal{H}}^m,Q_{\mathcal{H}}^l)$$\left(Q_{\mathcal{H}}^{j}, Q_{\mathcal{H}}^{m}, Q_{\mathcal{H}}^{l}\right)$组成，其中，$Q_{\mathcal{H}}^j$$Q_{\mathcal{H}}^{j}$表示在$Q_{\mathcal{H}},Q_{\mathcal{H}}^m$$Q_{\mathcal{H}}, Q_{\mathcal{H}}^{m}$中的最接近点，$P_{\mathcal{H}}^{i^{\prime }}$$P_{\mathcal{H}}^{i^{\prime}}$表示位于相邻两个激光通道中的最近点，$Q_{\mathcal{H}}^l$$Q_{\mathcal{H}}^{l}$表示与$P_{\mathcal{H}}^{i^{\prime }}$$P_{\mathcal{H}}^{i^{\prime}}$位于同一激光通道中的次近邻点。PNN-C点$(Q_{\mathcal{H}}^{j^{\prime }},Q_{\mathcal{H}}^m,Q_{\mathcal{H}}^l)$$\left(Q_{\mathcal{H}}^{j^{\prime}}, Q_{\mathcal{H}}^{m}, Q_{\mathcal{H}}^{l}\right)$确定了$P_{\mathcal{H}}^{i^{\prime }}$$P_{\mathcal{H}}^{i^{\prime}}$的对应平面，如蓝色三角形所示。

3. ENN-C是指识别最近的两个边缘点作为查询边缘点的对应边线。在图4中，查询边缘点$P_{\mathcal{E}}^{i^{\prime }}$$P_{\mathcal{E}}^{i^{\prime}}$的ENN-C点由$(Q_{\mathcal{E}}^{j^{\prime }},Q_{\mathcal{E}}^m)$$\left(Q_{\mathcal{E}}^{j^{\prime}}, Q_{\mathcal{E}}^{m}\right)$组成，这确定了$P_{\mathcal{E}}^{i^{\prime }}$$P_{\mathcal{E}}^{i^{\prime}}$的对应边线，如蓝色线所示。 第三，计算源特征点与其匹配之间的对应点之间的距离。到其对应边线和平面的距离分别表示为${\mathrm{d}}_{\mathcal{E}}^i$$\mathrm{d}_{\mathcal{E}}^{i}$和${\mathrm{d}}_{\mathcal{H}}^i$$\mathrm{d}_{\mathcal{H}}^{i}$，如图4所示。值得注意的是，只有在特定范围内的邻居才被认为是有效的。如果最近邻点与查询点之间的距离超过预定义阈值$r_{in}$$r_{i n}$，则将查询点视为异常值并排除在外，以确保它不会影响配准结果。该阈值范围定义为$r_{in}$$r_{i n}$，保证所有相关的邻居都被包括进来，而超出$r_{in}$$r_{i n}$的点被忽略。

4. 运动估计模块：第三模块专注于使用对应关系进行运动估计。该过程首先构建一个非线性最小二乘函数来测量配准误差，并采用Levenberg-Marquardt算法迭代优化初始变换矩阵得到最优矩阵$T_{\text{opt }}$$T_{\text {opt }}$。这个最优矩阵确保转换后的源点云（表示为$T_{\text{opt }}\cdot P$$T_{\text {opt }} \cdot P$）与目标点云$Q$$Q$之间的最大对齐，如图1所示。此外，如[1]所述，迭代次数设置为2，这意味着每次配准过程包括构建一次搜索结构和执行两次对应关系搜索。

B. 相关工作

在本小节中，我们介绍点云配准算法的相关工作，涉及搜索结构优化、搜索算法改进和硬件加速。

在搜索结构优化方面，树结构，尤其是KD树、局部敏感哈希和溢出树，在点云配准中被广泛使用。根据一项比较研究[9]，KD树在精度、构建时间、搜索时间和内存使用方面具有显著优势。然而，在处理自动驾驶场景中常见的稀疏且不均匀的点云时，构建和搜索过程的效率会显著下降。为了有效管理这类点云，开发了新颖的空间分区结构，如双分割体素结构（DSVS）[5]和占用感知体素结构（OAVS）[6]、[12]、[18]。这些方法将点云分割成三维立方体空间，即体素（voxels），消除了空体素，并继续分割占据的体素，随后按体素的哈希值对点进行组织。尽管这些方法在构建时间和内存使用方面具有显著优势，但由于每个体素中的点数和邻近体素的数量是可变的，导致搜索速度相对较慢。

在搜索算法优化方面，一些研究[7]、[11]、[19]、[20]采用了近似搜索方法，例如范围搜索或概率分布搜索，这大大减少了搜索时间，最多可以减少两个数量级。然而，这些方法往往会牺牲准确性和鲁棒性。为了在不牺牲准确性的情况下提高搜索效率，一些研究[12]、[21]-[23]专注于优化数据访问策略。探索的技术包括缓存搜索结果以提高后续搜索的命中率或将点聚合以便并行访问。然而，这些方法引入了点重新排序或调度的额外时间开销。此外，必须利用对应搜索任务中固有的特定特征，特别是对应点的局部性和几何特征，以显著提升搜索效率。

在硬件加速方面，FPGA和GPU已被广泛用于加速配准算法。研究[13]、[24]、[25]展示了在GPU上使用高度并行策略高效构建KD树和K近邻搜索。然而，基于GPU的方法通常面临高能耗问题，从而降低其能效。相比之下，基于FPGA的解决方案提供了更高的能效。一些工作[5]、[8]、[9]、[26]-[28]采用了可重用的多级缓存机制、关键帧调度策略以及高度并行的排序与选择电路，以提高实时性能。尽管取得了这些进展，但大多数努力集中在优化搜索加速器上，而忽略了其他组件的执行时间和数据传输开销，限制了整体效率。为了解决这些问题，一些研究[6]、[15]将配准算法分为硬件和软件组件，利用协同优化方法减少冗余搜索操作并提高效率。同时，其他工作[10]、[14]、[29]在算法、架构和缓存层面优化结构构建过程和K近邻搜索，实现了高度可配置和超快速的K近邻加速器。然而，大多数依赖于近似搜索方法，这些方法过滤掉许多邻近点，未能满足LSLAM（Lightweight Simultaneous Localization and Mapping）系统严格的精度要求。此外，几乎所有现有的方法都没有结合搜索结构的几何属性，导致平面和边缘对应搜索效率较低。

III. 所提配准框架的概述

本节提供所提出的RPSCS（基于RPS结构的协同软硬件设计配准框架）的概述。基于第二部分A节的分析，我们介绍了该框架的关键组件，包括RPS（Radial-Planar-Sector）结构、基于RPS的对应搜索算法、RPS-CS加速器以及协作式配准流程。

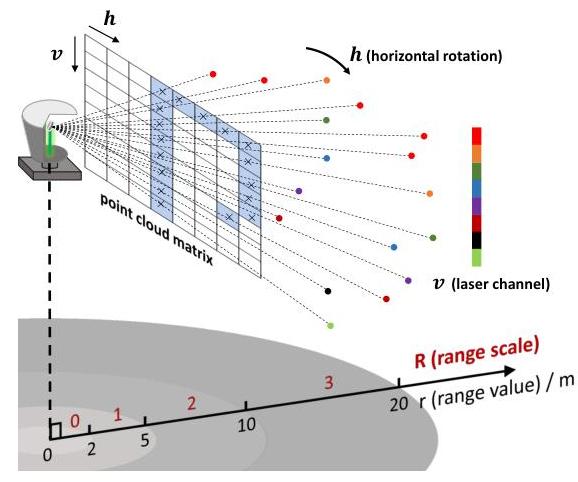
图5. 通过RPS结构分割点云的示意图。相同颜色的点是来自相同激光通道的测量数据。

A. RPS结构和RPS-CS算法概述

为了利用对应点的局部性和几何特征，我们提出了一种称为RPS的新搜索结构，如图5所示。RPS结构通过以下工作流程将点云数据组织成一种高效的格式，以进行对应搜索：

• 首先，RPS结构将点云投影到矩阵格式中，其中行对应激光通道，列对应水平扫描角度。此过程创建了数据的结构化表示，图5中的蓝色网格指示了投影位置。

• 其次，根据点到LiDAR传感器的距离（范围值）将投影点分割成不同的距离区间（range scales）。每个距离区间对应一个特定的范围值区间，通过行、列和距离区间索引实现点的精确定位。图5说明了范围值与距离区间之间的关系。

• 第三，我们将点云矩阵分割成一组距离区间分割域（RSSD），其中具有相似距离区间的点被重新排序为连续的内存块，采用计数排序（counting sort）算法。生成的RPS结构包含两个关键组件：存储重新排序点的RPS-Points，以及记录每个距离区间起始索引的RPSIndex。图7提供了该结构的详细示例。 基于RPS结构，我们提出了一种高效且灵活的对应点搜索算法，称为RPSCS，用于在指定搜索半径内识别各种类型的对应点 $r_{in}$$r_{i n}$ 。RPS-CS算法执行以下五个步骤：

• 首先，通过计算查询点的行和列索引（基于其水平扫描角度和激光通道）及其基于范围值的距离区间索引来确定查询点的RPS位置。距离区间索引是通过预定义的查找表（LUT）获得的。

• 其次，根据查询点的位置和搜索半径 $r_{in}$$r_{i n}$ 确定搜索区域，如公式（5）所示。该区域表示为一系列

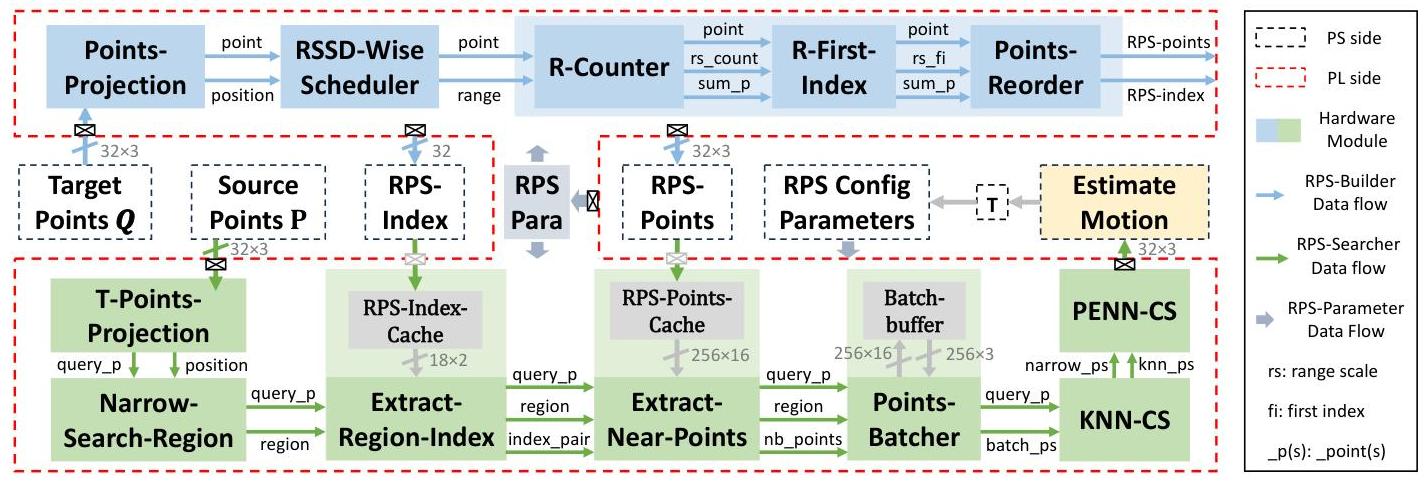
图6. 所提出的RPS-CS加速器和基于RPS-CS的软硬件协同设计配准框架示意图。

RPS-Index对，其中每一对指定RPS-Points中的点子集。

• 第三，从RPS结构中提取候选对应点。对于每个有效的RPS-Index对，由于相似距离区间的点已通过重新排序形成连续内存块，因此这些点可以并行检索。

• 第四，算法使用高度并行的K选择方法从候选点中识别K近邻对应点（KNN-C）。如果搜索目标仅限于KNN-C，则直接返回结果。否则，进一步筛选候选点以获取特定几何特征。

• 最后，使用筛选后的点来搜索其他类型的对应点，例如最邻近对应点（PNN-C）或扩展邻近对应点（ENN-C）。这些附加对应点由快速基于激光通道（laser channel）的条件K选择方法计算得出，如算法2所示。

B. 基于RPS-CS的注册框架概述

除了优化搜索结构和搜索算法外，我们还提出了一种软硬件协同设计的注册框架，以进一步提升性能。该框架基于异构系统架构，结合了高性能处理系统（PS）和单个FPGA板上的用户可编程逻辑（PL）。该框架的结构设计和操作流程如图6所示。

在PL侧，我们实现了一个RPS-CS加速器，包含两个主要组件：RPS构建器和RPS搜索器。

• RPS构建器：此组件负责使用数据流架构构建RPS结构，由图6中的蓝色块表示。对于每个RSSD中的点，该模块负责以下操作：将目标点投影到矩阵格式，按RSSD分组形成数据流，计算每个范围层级内的点数，计算每个范围层级的起始索引，并相应地重新排序点。这种并行化过程确保了高效的RPS结构生成。

• RPS搜索器：此组件旨在执行快速且可配置的对应关系搜索，重点是内存效率和并行性，由图6中的绿色块表示。搜索过程分为七个模块：将查询点投影到RPS结构中，缩小搜索区域，提取RPS-Index对，并行提取每一对中的点，将接近的点聚集成批次，使用高度并行的K-选择电路搜索K-Nearest Neighbor Candidates (KNNC)，以及使用基于激光通道的K-选择电路识别Pseudo Nearest Neighbor Candidates (PNN-C) 和 Exact Nearest Neighbor Candidates (ENN-C)。这种模块化设计确保了高效率和适应各种对应关系搜索任务的能力。

此外，RPS参数配置模块配置了RPS-CS加速器中的所有模块，以支持多模式操作和自定义优化功能。它能够在RPS构建器和RPS搜索器组件之间切换，并根据不同的对应关系类型调整参数，例如搜索区域大小。

在PS侧，框架管理点云数据存储、RPS结构信息、运动估计和协同配准工作流程的整体控制，如第二节A部分所述。

PS和PL侧之间的所有接口都使用流式FIFO端口实现，并通过数据打包提升传输效率。在加速器内部，数据以定点格式表示，而在加速器外部，则以浮点格式表示。数据类型转换过程如图6中的端口图标所示。我们使用Xilinx Vitis 高层次综合（HLS）工具生成了FPGA的寄存器传输级（RTL）模型。同时，我们整合了一个动态电压调整模块[30]以优化能量效率。

IV. 高效构建RPS搜索结构

在本节中，我们首先介绍构建RPS结构（Range Scale Partitioning Structure）的细节。然后，我们提出RPS-Builder加速器的硬件实现。

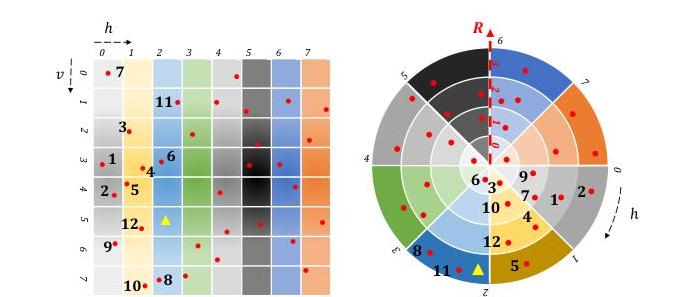
(a) 点云的侧视图 (b) 点云的顶视图

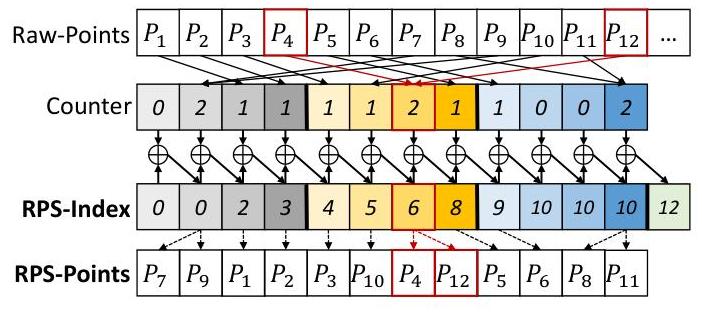
(c) 使用计数排序算法推导《RPS》结构

图7. 构建《RPS》搜索结构的一个示例。“‘ $R$$R$ ’”表示范围尺度。

A. 构建《RPS》搜索结构

由于《RPS》搜索结构根据投影位置和范围值对点云进行分割，因此构建《RPS》结构有三个阶段。首先，通过将点投影到矩阵的方式分割点云。如图7(a)所示，原始点云被组织成一个RSSD方式矩阵，采用了一种低复杂度但精确的投影方法[30]。其次，根据范围值分割点云矩阵。我们以RSSD方式遍历点云矩阵，计算每个点的范围值。这些范围值代表了每个点到激光雷达传感器的距离。随后根据这些值，我们将每个预定义域内的点分割成不同的范围尺度，如图7(b)所示。最后，使用计数排序算法推导《RPS》搜索结构。《RPS》结构包含两个关键组件：重新排序的点（《RPS-Points》）和每个范围尺度的第一个索引（《RPS-Index》）。相邻《RPS-Index》值之间的数值差值对应每个相应范围尺度内的点数。图7(c)给出了《RPS-Points》和《RPS-Index》的一个示例。

1. 通过将点投影到矩阵的方式分割点云：考虑到帧点云是在360°水平旋转扫描期间捕获的，将点云投影到矩阵中是可行的。矩阵的尺寸为 $V\times H$$V \times H$ 。这里， $V$$V$ 表示激光通道的数量， $H$$H$ 表示从每个激光通道在整个360°水平旋转过程中获得的测量点数。 $H$$H$ 的值通过公式（公式内容）计算得出，其中 $\mathrm{\Delta }\alpha$$\Delta \alpha$ 表示水平旋转的平均角分辨率。

给定点 $p(x,y,z)$$p(x, y, z)$ ，行和列索引 $(v,h)$$(v, h)$ 由方程（2）计算得出，其中 $\mathrm{\Delta }\omega$$\Delta \omega$ 是平均角分辨率。

算法 1 通过计数排序算法获得 RPS 点 输入：点云矩阵 $PCM[H][V]$$P C M[H][V]$ 输入：RPS 索引 $RPSI[H][M]$$R P S I[H][M]$ 输出：RPS 点 $RPSP\left[N_Q\right]$$R P S P\left[N_{Q}\right]$ : 重置范围尺度占用计数器 $\mathrm{RSOC}[\mathrm{H}][\mathrm{M}]=0$$\operatorname{RSOC}[\mathrm{H}][\mathrm{M}]=0$ : 重置重新排序索引 $\mathrm{RI}=0$$\mathrm{RI}=0$ 对 PCM 中的每个 RSSD 执行 $$$\quad$ 对 RSSD 中的每个点执行 $$$\quad$ 获取范围尺度 $R$$R$ 的值 $PC{M}_{ij}$$P C M_{i j}$ 如果 $R\in [0,M)$$R \in[0, M)$ 则过滤空元素 RI $\leftarrow \mathrm{RPSI}[i][\mathrm{R}]+\mathrm{RSOC}[i][\mathrm{R}]$$\leftarrow \operatorname{RPSI}[i][\mathrm{R}]+\operatorname{RSOC}[i][\mathrm{R}]$ $\mathrm{RSOC}[i][\mathrm{R}]\leftarrow \mathrm{RSOC}[i][\mathrm{R}]+1$$\operatorname{RSOC}[i][\mathrm{R}] \leftarrow \operatorname{RSOC}[i][\mathrm{R}]+1$ RPSP[RI] $\leftarrow PC{M}_{ij}$$\leftarrow P C M_{i j}$ 结束如果 结束对于 结束对于 垂直方向上相邻激光通道之间的分辨率。

为了高效计算 $(v,h)$$(v, h)$，我们提出了一种基于我们先前研究 [30] 的改进方法，该方法通过两个查找表（LUT）快速准确地获取行和列索引。最初，使用公式（3）分别计算垂直和水平查找值，分别记为 $a_v$$a_{v}$ 和 $a_h$$a_{h}$。然后，这些值用于从两个预定义的 LUT 中检索相应的行和列索引。LUT 特别设计以考虑激光通道的垂直角度和水平旋转角度，确保数据准确性和算法高效性。

图 7(a) 给出了一个点云矩阵的例子，其中黄色三角形的坐标 $(v,h)$$(v, h)$ 被确定为 $(5,2)$$(5,2)$。

由于激光雷达（LiDAR）点云在近距离密集、远距离稀疏且分布不均匀，我们引入范围尺度概念进一步分割点云矩阵。此过程包括两个主要步骤：

范围值的计算：给定点 $p(x,y,z)$$p(x, y, z)$，我们首先通过公式（3）计算范围值 $r$$r$。该值计算了点 $p$$p$ 到激光雷达（LiDAR）传感器的距离。

使用范围尺度进行分割：接下来，我们引入范围尺度将范围空间划分为若干区间。假设激光雷达（LiDAR）的最大检测范围是 $r_{max}$$r_{\max }$ 米，我们将范围空间划分为 $M$$M$ 个范围尺度区间。$r_{max}$$r_{\max }$ 的值通常从激光雷达（LiDAR）的数据表中获得，而 $M$$M$ 是根据点云分布特性和实验分析确定的。随后，构建了一个非均匀范围尺度查找表（RLUT），以关联不同的范围值与对应的范围尺度。

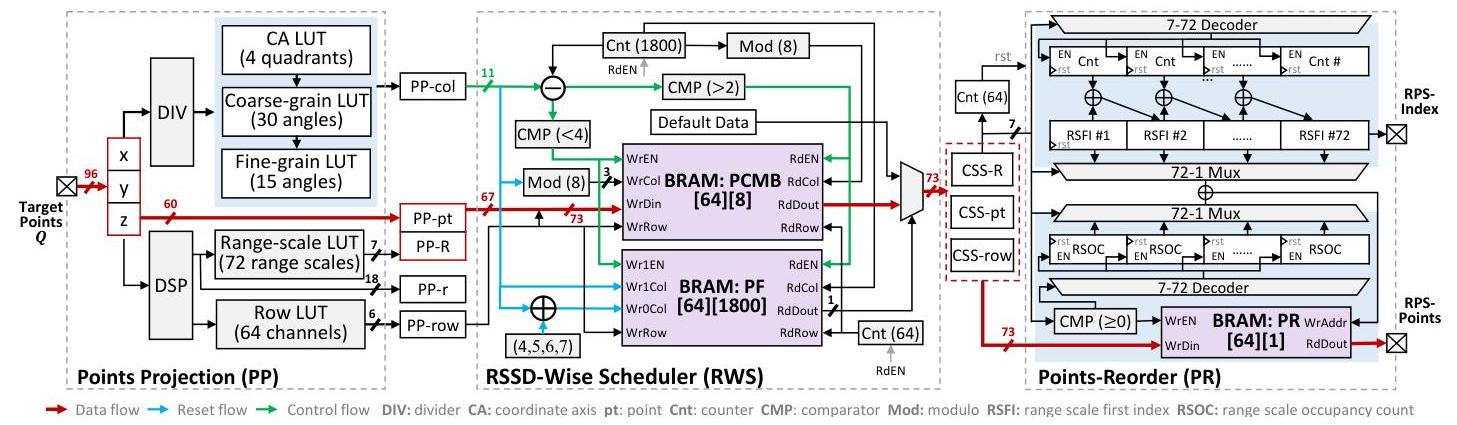
图8. RPS-Builder加速器的硬件架构。 相应的范围尺度。图5说明了范围值 $(r)$$(r)$ 和范围尺度 $(R)$$(R)$ 之间的关系，其中最大范围值 $\left(r_{max}\right)$$\left(r_{\max }\right)$ 设置为20米且 $M$$M$ 等于4。每个 $R_i$$R_{i}$ 对应区间 $[r_i,r_{i+1})$$\left[r_{i}, r_{i+1}\right)$ 。在图7(a)中，黄色三角形的范围尺度 $R$$R$ 为3。

因此，我们可以获得具有属性 $(x,y,z,r,R)$$(x, y, z, r, R)$ 的增强点云矩阵。此外，空元素用 $(0,0,0,-1,-1)$$(0,0,0,-1,-1)$ 进行填充。3）推导RPS搜索结构：为了构建RPS搜索结构，我们利用基于点云矩阵和范围尺度的流式计数排序算法。首先，定义RSSD以将点云矩阵划分为区域，每个RSSD包含 $N_{sd}$$N_{s d}$ 列。图7(a-b)突出显示了八个不同的RSSD，每个都用不同颜色表示。其次，分三步对每个RSSD应用计数排序方法：

1. 计算每个范围尺度中的点数。前三个RSSD的计数结果如图7(c)所示。

2. 计算RPS-索引，它指示每个范围尺度在重新排序的RPS-Points中的起始索引位置。这是通过累计求和实现的，如图7(c)所示。

3. 根据范围尺度和RPS-索引重新排列点以生成RPS-Points。算法1详细描述了此过程，图7(c)提供了一个示例。

重新排序后的目标点云，称为RPSPoints，保留与原始点云相同的大小，但具有 $(x,y,z,r,R,v)$$(x, y, z, r, R, v)$ 特征。RPS-索引的大小是 $M\times H/N_{sd}$$M \times H / N_{s d}$ ，反映了通过范围尺度和RSSD对点云的分割。

ENN-C的特殊处理：边缘特征点需要表现出更高的曲率。如[30]所述，来自同一扫描激光束的两个连续边缘特征点之间的距离大于5个单位。为了优化ENN-C的搜索结构，我们将映射点云矩阵的大小调整为 $M\times H/N_{sd}/5$$M \times H / N_{s d} / 5$ 。这一修改显著缩小了ENN-C搜索过程中的搜索空间，提高了计算效率。

B. 构建RPS的硬件加速器

在本小节中，我们介绍了在所提出的RPSBuilder加速器中实施的硬件设计和优化策略。我们专注于提高性能的同时减少硬件资源的使用。

在架构层面，我们为加速器设计了一个高效的任务级流水线设计，如图8中的红线所示。该过程首先将目标点转换为矩阵格式，随后按照RSSD的顺序进行调度，并最终重新排序到RPSPoints数组中。

为了简化架构图，我们设置参数为$M=72,H=1800$$M=72, H=1800$和$V=64$$V=64$。此外，R-Counter和R-First-Index模块被合并到Points-Reorder模块中。因此，RPS-Builder加速器被划分为三个不同的模块：Points-Projection（PP）模块（点投影模块）、RSSD-Wise Scheduler（RWS）模块（基于RSSD的调度器模块）和Points-Reorder（PR）模块（点重排序模块）。

1. Points-Projection（PP）模块（点投影模块）：该模块旨在优化硬件资源效率的同时保持高吞吐量的流水线架构。我们采用基于坐标和多分辨率的LUT方法来实现这种平衡，如图8所示。

为了高效地在包含1800个条目的LUT表中查找列索引，我们利用了一种基于坐标和多分辨率的LUT方法，该方法包含四个关键步骤。首先，我们计算查找值$a_h$$a_{h}$，使用除法器测量每个点的水平角度。其次，我们使用一个紧凑的、4项坐标轴LUT通过$x$$x$和$y$$y$值识别水平角度所在的象限。第三，我们通过粗粒度30项LUT细化查找区域。最后，在这个缩小的区域内，通过细粒度LUT查找最终确定列索引$h$$h$。

考虑到距离尺度LUT和行LUT的大小相对较小，我们为它们各自的用途实现了单独的、隔离的LUT。这两个LUT的大小分别配置为72和64，这对应于距离尺度的数量和激光通道的数量。2. RSSD-Wise Scheduler（RWS）模块（基于RSSD的调度器模块）：尽管采用了基于高精度LUT的投影方法，但投影点的排序并不严格遵守RSSD-wise顺序。无序且分散的点会降低加速器的效率。因此，我们开发了一个高效的RWS模块，该模块利用紧凑的点云矩阵缓冲区（PCMB）和高吞吐量的流水线架构，确保输出点严格遵守RSSD-wise顺序。实现过程中面临三大主要挑战：

• 确定PCMB的大小：广泛的实验分析使我们将PCMB列的大小设置为8。这个大小是最优的，可以防止输入点覆盖尚未输出的点。

• PCMB输入和输出的管道调度：我们通过比较写入和读取列（如图8中标注的绿线所示）来动态管理PCMB的读写操作。此机制在输出队列过载时停止新点的输入，从而保持管道结构的高性能。

• 防止覆盖待输出的点：实现了一个大小为 $64\times 1800$$64 \times 1800$ 的1位投影标志（PF）寄存器数组，用于跟踪元素是否已被投影。如果已投影，则从PCMB中输出数据；否则，输出默认数据，其范围尺度设为-1。此外，如图8中的蓝线所示，我们在管道结构中引入了PF数组的复位过程以优化延迟。该过程持续复位输入列后方4至8列的元素。

3. 点重排序模块：该模块有效实现了使用高吞吐量的管道结构的计数排序算法。如图8所示，我们的设计包括72个点计数器、72个范围尺度首次索引（RSFI）触发器（FF）和72个范围尺度占用计数（RSOC）计数器。数字72对应于我们设计中的 $M$$M$ 值。这些组件共同促进了RSSD中所有64个点的重新排序，从而确保高效的并行处理。

V. 快速可配置的对应搜索

在本节中，我们首先介绍基于RPS结构的KNN-C、PNN-C和ENN-C搜索过程。随后，我们提出RPS-Searcher加速器的硬件实现。

A. 基于RPS的多类型对应搜索

从第二节A部分可知，PNN-C被识别为最复杂的对应类型，因为它涵盖了KNN-C和ENN-C的搜索过程。因此，我们以PNN-C为例，说明基于RPS结构和搜索范围（ $r_{in}$$r_{i n}$ ）的搜索过程。

对于查询点 $P_{\mathcal{H}}^i$$P_{\mathcal{H}}^{i}$ ，PNN-C由点 $(Q_{\mathcal{H}}^j$$\left(Q_{\mathcal{H}}^{j}\right.$ 和 $Q_{\mathcal{H}}^m,Q_{\mathcal{H}}^l)\in Q_{\mathcal{H}}$$\left.Q_{\mathcal{H}}^{m}, Q_{\mathcal{H}}^{l}\right) \in Q_{\mathcal{H}}$ 组成。搜索过程包括五个步骤，如图9所示：

1. 确定查询点的RPS位置：计算查询点的RPS位置（包括行索引 $v_i$$v_{i}$ 、列索引 $h_i$$h_{i}$ 和范围尺度 $R_i$$R_{i}$ ），如第IV节所述。例如，在图9（a）和（b）中，查询点（红色星形）的RPS位置为 $(3,1,2)$$(3,1,2)$ 。

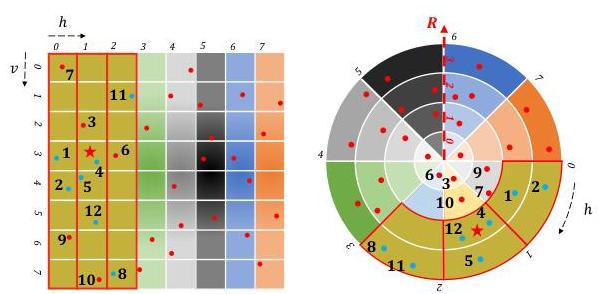
（a）点云侧视图 （b）点云顶视图

（c）三个搜索块的示意图

（d）候选对应点的示意图

图9。基于RPS的对应搜索示例。这些图改编自[31]。

2）计算搜索区域：将搜索区域定义为以$(v_i,h_i,r_i)$$\left(v_{i}, h_{i}, r_{i}\right)$为中心的立方体，边长为$2r_{in}$$2 r_{i n}$。首先，通过公式（4）和基于$r_i$$r_{i}$的查找表（LUTs）确定对应搜索区域尺寸$h_{sr}$$h_{s r}$、$=[h_{min},h_{max}]$$=\left[h_{\min }, h_{\max }\right]$和$R_{sr}=[R_{min},R_{max}]$$R_{s r}=\left[R_{\min }, R_{\max }\right]$。例如，红色星标的搜索区域是$h_{sr}=[0,2]$$h_{s r}=[0,2]$和$R_{sr}=[2,3]$$R_{s r}=[2,3]$，如图9（a-b）所示。其次，使用公式（5）定义搜索块$(SB=[S{B}_{min},S{B}_{max}))$$\left(S B=\left[S B_{\min }, S B_{\max }\right)\right)$。例如，图9（c）将搜索块定义为区间$[2,4),[6,9)$$[2,4),[6,9)$和$[10,12)$$[10,12)$。

3. 在搜索区域内提取候选对应点：根据搜索块从RPSPoints数组中提取相关点，将其指定为候选对应点。图9（d）用红色矩形突出显示了搜索块内的点。结构化的RPS-Points数组支持在每个块内并行提取点。

4. 在候选对应点中搜索KNN-C：在每个搜索块内，计算查询点到候选点的平方距离，选择KNN点，这些点作为候选几何点流向后续步骤。采用优先队列[30]搜索所有候选点中的KNN-C，识别最近邻点为$Q_{\mathcal{H}}^j$$Q_{\mathcal{H}}^{j}$。

5. 从候选点中搜索PENN-C（条件近邻对应点）。与优先队列K选择方法[30]不同，我们提出了一种快速条件K值选择方法，利用激光通道信息和按距离排序的候选点高效选择$Q_{\mathcal{H}}^m$$Q_{\mathcal{H}}^{m}$和$Q_{\mathcal{H}}^l$$Q_{\mathcal{H}}^{l}$，如算法2详细说明。

算法2 基于激光通道的并行条件优先队列K值选择方法，用于流式批量点处理

输入：候选几何点$\mathrm{GP}\left[N_g\right]$$\mathrm{GP}\left[N_{g}\right]$，范围参数为$.r$$. r$，行索引为$.v$$. v$，RPS索引为$.i$$. i$；最近邻点为$Q_j$$Q_{j}$
输出：$\mathrm{PNN}-\mathrm{C}:Q_l$$\mathrm{PNN}-\mathrm{C}: Q_{l}$和$Q_m$$Q_{m}$

1
for \(i \in\left[0, N_{g}\right)\) parallel do \(\quad »\) For All Points in GP
2
    gap of column index: \(G_{v}[\mathrm{i}] \leftarrow \operatorname{abs}(\mathrm{GP}[\mathrm{i}] \cdot \mathrm{v}-Q_{j} \cdot \mathrm{v})\)
3
    gap of RPS-index: \(G_{i}[\mathrm{i}] \leftarrow \operatorname{abs}(\mathrm{GP}[\mathrm{i}] \cdot \mathrm{i}-Q_{j} \cdot \mathrm{i})\)
4
    set the compare array \(C_{j}\) and \(C_{m}\) to \(\{-1\}\)
5
    for \(j \in\left[0, N_{g}\right)\) parallel do \(\quad »\) Conditional Compare
6
        \(C_{m}[\mathrm{i}] \leftarrow\) compare i and j, \(G_{v}[\mathrm{i}]\) and \(G_{v}[\mathrm{j}]\)
7
        \(C_{j}[\mathrm{i}] \leftarrow\) further compare \(G_{i}[\mathrm{i}]\) and \(G_{i}[\mathrm{j}]\)
8
    end for
9
    if \(C_{j}[\mathrm{i}]=0 \& \mathrm{GP}[\mathrm{i}] \cdot \mathrm{r}<Q_{l} \cdot \mathrm{r} \& G_{v}[\mathrm{i}]=0 \& G_{i}[\mathrm{i}]>0\) then
10
        \(Q_{l} \leftarrow \mathrm{GP}[\mathrm{i}]\)
11
    end if
12
    if \(C_{m}[\mathrm{i}]=0 \& \mathrm{GP}[\mathrm{i}] \cdot \mathrm{r}<Q_{m} \cdot \mathrm{r} \& 0<G_{v}[\mathrm{i}]<3\) then
13
        \(Q_{m} \leftarrow \mathrm{GP}[\mathrm{i}]\)
14
    end if
15
end for

对于$\mathrm{PNN}-\mathrm{C}$$\mathrm{PNN}-\mathrm{C}$的方法可以适应其他类型的对应：

• 对于KNN-C：跳过步骤5，在步骤4直接输出KNN对应。

• 对于ENN-C：修改步骤5以识别$Q_E^m$$Q_{E}^{m}$并将列索引$h$$h$除以5（单位：像素/元素，对应点云矩阵尺寸的缩小），以考虑专门的ENN-C RPS结构中点云矩阵尺寸减小的情况。

B. RPS-Searcher的硬件实现

本小节概述了所提出的RPS-Searcher加速器的硬件架构和优化策略，该加速器在保持高搜索精度的同时提升了任务级流水线吞吐量。基于第五节A部分中的搜索算法，该加速器包含七个模块：Transform-Points-Projection（TPP）、Compute-SearchRegion（CSR）、Extract-Region-Index（ERI）、Extract-NearPoints（ENP）、Points-Batcher（PB）、KNN-CS和PNN-CS，如图6所示。以下是每个模块的关键优化细节。

1. TPP模块：TPP模块将源点转换到目标坐标系，并将查询点投影到RPS结构中。应用了两种主要优化：

   • 位宽优化：源点的位宽优化为20位，确保足够精度，同时减少硬件资源占用。

   • 矩阵乘法展开操作：矩阵乘法过程完全展开以加速计算并提高硬件效率。

2. CSR模块：CSR模块计算查询点的搜索区域，由列索引表示。如图10所示，采用了一种基于邻近性的搜索优化策略，使用序列生成器（如图10所示）$(0,-1,1,-2,2,\dots )$$(0,-1,1,-2,2, \ldots)$

3. ERI模块：ERI模块从搜索区域中提取搜索块$(S{B}_{min},S{B}_{max})$$\left(S B_{\min }, S B_{\max }\right)$。实现ERI模块时面临两个挑战。(1) 片上内存容量不足以存储整个RPS-Index数组，访问外部内存会引入显著延迟。(2) 搜索区域内冗余点会降低搜索效率。为了解决这些挑战，如图10所示，我们提出了一种动态缓存策略，具体包含以下三方面：

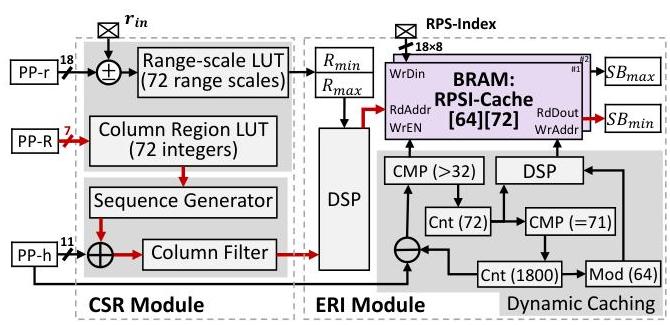
图10 CSR与ERI模块的硬件实现示意图。 优先检索邻近列的点。一旦收集足够目标点，即可跳过对距离较远列的搜索，从而提高效率。

• 优化的片上缓存：观察到RPS-Index和输入查询点都大致遵循RSSD的顺序，我们设计了一个片上滑动窗口缓存，称为RPSI-Cache（图6）。RPSI-Cache有两个关键特性：(1) 它是紧凑的，仅占用原始RPS-Index数组大小的大约 $3.5\mathrm{\%}$$3.5 \%$。这一缩小后的尺寸足以覆盖任何查询点的相邻搜索区域，这一点通过性能分析结果得到确认。(2) RPSI-Cache根据查询点的位置动态刷新，确保连续覆盖相邻区域。

• 高效的缓存刷新策略：当查询点的列索引超过当前读取列索引的预定义阈值时，我们用新数据刷新RPSI-Cache中过时的部分。这一策略对于保持ERI模块的高吞吐量流水线架构至关重要。为了进一步提高性能，RPSI-Cache被循环划分为多个段，并绑定到2端口BRAM，使得可以同时并行读写多个RPSI值。

4. ENP模块：ENP模块旨在从RPS-Points数组中基于识别的搜索块提取候选对应点。为了增强效率，我们也采用了动态缓存策略，同时进一步优化了点的读取并行性以满足性能要求。我们将4个候选点打包成RPSP-Cache数组中的一个大位宽的单个元素，并将数组划分为16个独立段，从而实现48个候选点的并行读取。

5. PB模块：PB模块将数量可变的候选点聚合为固定大小的数据批次，以便在后续KNN-CS模块中进行高效的密集计算。

这种设计的动机在于单个输入的候选点数量高度可变，范围在1到48之间。直接传输多达48个点到下一阶段通常需要填充无效数据，这会引入低效性，如硬件资源浪费、功耗增加以及时钟路径延长，这些都会降低时序性能。同时，丢弃多余的点会损害搜索精度，因为可能会丢失关键数据。

为了解决这个问题，我们提出了一种动态分组与批处理策略，该策略可以根据RSSD中变化的候选点数量对其进行调整，并将其打包成符合下一模块要求的固定大小的数据批次。通过动态管理数据缓冲和输出，PB模块确保搜索精度保持不变，同时优化资源利用率并减少开销。

高效缓冲利用移位批处理缓冲器在流水线架构中实现该模块，同时最小化硬件资源消耗。缓冲区大小为 $256\times 64$$256 \times 64$ ，由一个跟踪有效候选点数量的指针控制。传入数据存储在指针指示的位置，被新有效点覆盖，确保内存的有效使用。一旦指针超过预定义阈值，模块将输出密集批次的点到下一阶段，并重置指针以开始新批次处理。这种设计不仅确保了高吞吐量；同时最小化资源使用。

6. KNN-CS模块：KNN-CS模块专注于根据候选对应点与查询点的距离对其进行排序，并选择K个最近邻（K近邻）以识别 $Q_H^l$$Q_{H}^{l}$ 。

从流式候选点中排序和选择K近邻点计算成本较高，因为需要大量的比较操作和过度的数据带宽消耗。一种朴素的排序方法将导致硬件复杂度和功耗增加。

为了解决这个问题，我们采用了一种基于K选择的优先队列优化方法，该方法能够高效地选择和排序K近邻点，同时减少比较器的数量并降低数据带宽需求。当候选点流入模块时，使用并行比较网络从传入数据中选择K近邻点，显著减少了数据带宽。然后，这些K近邻点与优先队列中的内容进行比较，优先队列容量同样设定为K，以更新队列。一旦所有候选点都被处理完毕，优先队列将包含最终的K近邻对应关系。

通过采用我们在先前工作[30]中提出的高效优先队列架构，这种方法减少了硬件资源使用和降低功耗，同时提升后续阶段的性能。

7. PENN-CS模块：PENN-CS模块负责从候选几何点中选择PNN-C或ENN-C对应点。选择过程在计算上是密集的，因为它通常需要大型比较器阵列和资源密集型的有序比较来找到所需点。此外，无序的几何点使选择过程效率降低，增加了资源利用率和处理时间。

为了优化这一过程，我们利用激光通道信息和K近邻点的有序性质来提高效率并减少硬件需求。该模块采用了两种关键策略：

• 使用激光通道属性进行高效的点选择：与之前依赖大比较器阵列的方法[30]不同，我们利用搜索区域内的点的独特激光通道属性进行直接选择。搜索区域内的点属于同一列，并具有唯一的激光通道索引（行索引），并且 $Q_H^m$$Q_{H}^{m}$ 的激光通道与 $Q_H^l$$Q_{H}^{l}$ 匹配。基于这一观察，我们直接比较激光通道和距离以快速识别 $Q_H^m$$Q_{H}^{m}$ ，如算法2所述。这显著减少了比较器阵列的规模，同时提高了选择精度。

• 资源高效的比较逻辑优化：PENN-CS模块不是从无序的点中选择，而是从已经排序的KNN点中选择 $Q_H^m$$Q_{H}^{m}$ 。首先，根据激光通道和顺序索引，从输入的K个候选几何点中选择最合适的点 ${\tilde{Q}}_H^l$$\widetilde{Q}_{H}^{l}$ 。然后，将 ${\tilde{Q}}_H^l$$\widetilde{Q}_{H}^{l}$ 与当前 $Q_H^l$$Q_{H}^{l}$ 进行比较，较近的点保留到 $Q_H^l$$Q_{H}^{l}$ 中。这减少了所需的比较器的数量和位宽，大大减少了资源占用并提高了效率。 通过结合基于激光通道的选择和比较逻辑优化，PENN-CS模块在性能和资源效率之间实现了平衡，确保以最小的硬件资源消耗准确选择几何对应点。

VI. 实验结果与分析

在本节中，我们首先描述实验设置，包括测试数据集、测试用例、参数、各种实现方式和测试平台。随后，我们对不同对应搜索方法的运行时间、功耗和资源利用率进行比较分析。接下来，我们提供所提出的RPS-CS加速器的详细分析，包括各个模块的延迟和资源利用率。最后，我们将基于RPS-CS的注册框架集成到L-SLAM系统中，替换其现有的注册算法。这种集成使我们能够在实际应用场景中评估该框架对精度和运行时性能的影响。

A. 实验设置

实验数据集：为了评估所提出的点云RPS-CS加速器和注册框架，我们使用了KITTI数据集[10]，特别是2012年视觉里程计/SLAM评估点云。该数据集包括在真实驾驶场景中捕获的各种道路环境数据。在我们的评估中，我们仅关注由Velodyne HDL-64E LiDAR收集的点云，该传感器使用64个激光器，扫描频率为10 Hz。

表I 实验测试用例。

实验案例：为了全面评估所提出的RPS-CS加速器的性能，我们设计了四个具有代表性的实验案例，总结如表I所示。案例I采用来自先前工作的标准设置[5],[14]，作为比较的基线。案例II和案例III评估了在不同配置下的加速器的可扩展性和鲁棒性（具体配置参数为$N_P$$N_{P}$ 和 $N_Q$$N_{Q}$）。最后，案例IV通过分析典型点云配准任务中$N_P$$N_{P}$ 和 $N_Q$$N_{Q}$ 的平均数据量来评估RPS-CS加速器的实际应用性，如文献[1]所述。

对于所有案例，点云是从KITTI数据集中各种场景中的十个随机选择的连续帧点云中下采样得到的。

实验平台：基于ARM的测量是在配备Apple Silicon M4的Mac Mini（4.4 GHz）上进行的。FPGA实现使用Xilinx Vitis 2022.2开发，并在Xilinx UltraScale+ MPSoC ZCU104板（200 MHz）上验证。通过PMbus接口连接的嵌入式INA226传感器进行测量以获取FPGA平台的功耗；ARM平台的测量使用官方电源管理库API。所有测量都反映了整个平台的总功耗，以确保公平比较。

实验参数：根据KITTI数据集中使用的64线激光雷达的规格，我们仔细配置了实验参数。具体来说，我们确定水平分辨率$H=1800$$H=1800$ （ENN-C为360）和垂直分辨率$V=64$$V=64$ ，以便生成点云矩阵。此外，我们设定$N_{sd}=4,M=72$$N_{s d}=4, M=72$ 和$r_{in}=1$$r_{i n}=1$ 。这确保了对应搜索结果的准确性超过所有测试用例$95\mathrm{\%}$$95 \%$的阈值。

B. 运行时间、功耗和资源的比较

表II总结了测试案例I中各种对应搜索实现的每帧平均运行时间。FPGA上的PNN-CS时间是通过结合高并行k-选择实现方案[5]与KNN-CS时间数据得到的。原始PNN操作[1]的剖析显示，它平均搜索2,338个邻近点以针对每个查询点选择PNN对应关系。为了解决这个问题，我们开发了一个高并行k-选择加速器，可在21.9毫秒内完成对30,000个查询点各2,338个邻近点的处理。由于k选择加速器在任务级并行流水线中与原始KNN-CS加速器并行工作，最终PNN-CS时间取KNN-CS时间与21.9毫秒的较大值。

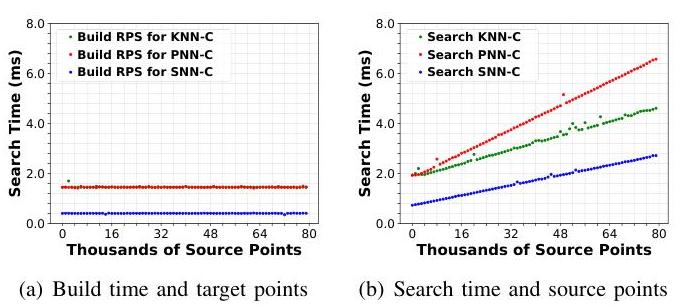
图11. RPS-CS加速器的性能结果。

实验结果表明，所提出的RPS-CS加速器实现了卓越的性能，在FPGA平台上仅需5.0毫秒即可构建结构并搜索30,000个点的PNN对应关系。与其他实现相比，我们的RPSCS加速器分别比QuickNN [14]、ParallelNN [9]和RPS-KNN [31]快$13.6\times ,7.5\times$$13.6 \times, 7.5 \times$倍、$4.7\times$$4.7 \times$倍。此外，RPS-CS加速器在数据结构构建时间和KNN/PNN对应搜索方面均达到最佳性能，验证了RPS结构的有效性和RPSBuilder和RPS-Searcher加速器的高并行性。

表II还比较了不同实现的平均功耗和能量消耗。以FLANN-CPU作为基线，能量效率比（EER）定义为实现的能量消耗与基线能量之比。RPS-CS加速器分别比QuickNN [14]、ParallelNN [9]和RPS-KNN [31]节能$20.7\times ,187\times$$20.7 \times, 187 \times$倍、$3.6\times$$3.6 \times$倍。这种能效主要归因于动态电压调节[32][33]，其中可编程逻辑（PL）侧的供电电压在固定200 MHz频率下动态调节，以在保持正确结果的同时最小化功耗。

由于性能（5.0毫秒）远超实时需求，我们专注于资源优化以进一步提高能效。表III显示了RPS-Builder、RPS-Searcher以及总RPS-CS加速器的完全布线资源利用率。与QuickNN相比，RPS-CS使用的可重构资源（LUT和FF）和DSP较少，但需要更多的内存来存储RPS-Points和RPS-Index数组。同样，RPS-CS使用的硬件资源少于DSVS，除了LUTs外。

C. RPS-CS加速器的详细分析

为了全面分析所提出的RPS-CS加速器，我们在测试用例II和III上评估其性能。图11显示了RPS结构构建和对应搜索期间的运行时间。

实验结果显示，RPS结构的构建时间对于KNN/PNN对应关系始终固定为1.4毫秒，对于SNN对应关系则为0.4毫秒。这种一致性是由于固定大小的点云矩阵组织（对于KNN/PNN为$V=64$$V=64$和$H=1800$$H=1800$的，对于SNN为$V=64$$V=64$和$H=450$$H=450$的）。基于该固定尺寸执行所有操作，确保构建时间保持固定。

表II 不同KNN/PNN对应搜索实现的比较

• PNN-CS时间基于高并行k值选择实现[5]和报告的KNN-CS时间。 ${}^{\ast }$${ }^{*}$ 总时间是构建时间和PNN-CS时间的总和。加速比是相对于基线的总时间。 EER（能量效率比）是相对于基线的能量。

表III 不同对应关系搜索加速器的资源利用率对比

搜索时间与源点数量几乎呈线性关系，表明RPS缓存[31]中的性能瓶颈已经解决。这一改进源于扩展了缓存端口位宽并优化了缓存策略以动态适配查询需求。然而，当查询数量低于3,000时，由于目标点数据量大导致的数据传输成为主导因素，$\mathrm{PNN}-\mathrm{C}$$\mathrm{PNN}-\mathrm{C}$和$\mathrm{KNN}-\mathrm{C}$$\mathrm{KNN}-\mathrm{C}$的搜索时间保持不变。超过这个阈值后，搜索时间成为主要因素，并随查询数量线性增长。

此外，这种线性增长的斜率由预设的最大搜索半径决定。由于KNN-C和ENNC具有相同的范围，它们的斜率几乎相同。相比之下，PNN-C需要更大的搜索半径来保持超过$95\mathrm{\%}$$95 \%$的精度，因此随着查询数量的增加，其斜率更陡峭，搜索时间的增长更快。

D. 注册框架评估

为了验证RPS-CS加速器在注册框架中的有效性，我们在测试案例IV中评估其运行时性能，并在集成到Simultaneous Localization and Mapping (SLAM)系统时评估其对准确性和速度的影响。

表IV 不同注册实现的准确性比较表

$t_{rel}$$t_{r e l}$：长度为$100\mathrm{m}-800\mathrm{m}$$100 \mathrm{~m}-800 \mathrm{~m}$的平均平移RMSE（%）。$r_{el}$$r_{e l}$：平均旋转RMSE（长度为$100\mathrm{m}-800\mathrm{m}$$100 \mathrm{~m}-800 \mathrm{~m}$）。

在案例IV中，RPS-CS加速器实现了与图11所示一致的运行时间。对于SNN-C，构建RPS结构需要0.4 毫秒，搜索对应关系需要0.6 毫秒。对于PNN和KNN的对应关系，构建时间为1.4 毫秒，搜索时间为1.9 毫秒。

为了评估准确性，将RPS-CS加速器集成到SLAM系统中，并通过以下实现评估定位轨迹的准确性：

• LOAM：原始LOAM[1]，在FPGA PS侧实现，作为基准。

• LOAM-RPS：在FPGA PS侧浮点RPS-CS集成的LOAM。

• LOAM-RPS-HW：在FPGA PL侧基于定点RPS的注册框架的LOAM。

这三种实现的准确性结果如表IV所示，使用官方KITTI评估工具进行评估。可以得出结论，我们提出的基于RPS的

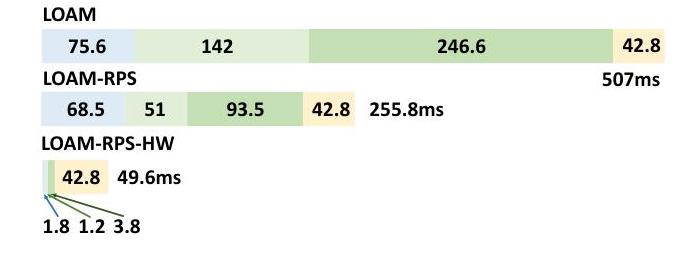
图12. 不同配准实现的运行时间比较。 配准框架对精度的影响可以忽略不计，观察到的精度下降约为 $1\mathrm{\%}$$1 \%$ 。在某些情况下，由于减少了异常对应点对，我们的框架可达到更高精度。 图12展示了在KITTI数据集上的平均配准时间。注册任务中的两次对应点搜索迭代使SNN和PNN的搜索时间分别达到1.2毫秒和3.8毫秒。基于RPS的配准算法在整体速度上实现了 $2\times$$2 \times$ 的提升，对应点搜索时间提高了 $2.7\times$$2.7 \times$ 。使用所提出的框架，整体运行速度提升了 $10.2\times$$10.2 \times$ ，达到20.1FPS，同时对应点搜索加速了 $68.2\times$$68.2 \times$ 。

VII. 结论

在这项工作中，我们提出了一种基于FPGA的实时点云配准框架，具有超快且可配置的对应点搜索能力。首先，我们开发了一种新颖的Range-Projection结构（RPS），将无序的LiDAR点云组织成矩阵格式，以实现高效的点定位，并将相邻点分组到连续内存块中以加速点访问。其次，我们引入了一种高效的多模式对应点搜索算法，利用RPS结构有效地缩小搜索区域，消除冗余点，并通过利用激光雷达特定的激光通道属性信息支持各种类型的对应关系。第三，我们设计了一个可配置的超快速RPS基础对应点搜索（RPS-CS）加速器，包括一个高性能的RPS构建器用于快速结构构建和一个高度并行的RPS搜索器用于快速对应点搜索，并通过动态缓存机制和流水线批处理模块来提升效率并增强可配置性。实验结果表明，与最先进的FPGA实现相比，RPS-CS加速器实现了 $7.5\times$$7.5 \times$ 的速度提升和 $17.1\times$$17.1 \times$ 的能效提升，而所提出的框架可处理64线激光雷达数据，实现了每秒20.1帧的实时性能。

参考文献

[1] J. Zhang and S. Singh, "Low-drift and real-time lidar odometry and mapping," Autonomous robots, vol. 41, no. 2, pp. 401-416, Feb 2017.

[2] X. Zhang and X. Huang, "Real-time fast channel clustering for lidar point cloud," IEEE Transactions on Circuits and Systems II: Express Briefs, vol. 69, no. 10, pp. 4103-4107, Oct 2022.

[3] C.-C. Wang, Y.-C. Ding, C.-T. Chiu, C.-T. Huang, Y.-Y. Cheng, S.-Y. Sun, C.-H. Cheng, and H.-K. Kuo, "Real-time block-based embedded cnn for gesture classification on an fpga," IEEE Transactions on Circuits and Systems I: Regular Papers, vol. 68, no. 10, pp. 4182-4193, Oct 2021.

[4] M. Muja and D. G. Lowe, "Scalable nearest neighbor algorithms for high dimensional data," IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 36, no. 11, pp. 2227-2240, Nov 2014.

[5] H. Sun, X. Liu, Q. Deng, W. Jiang, S. Luo, and Y. Ha, "Efficient fpga implementation of k-nearest-neighbor search algorithm for 3d lidar localization and mapping in smart vehicles," IEEE Transactions on Circuits and Systems II: Express Briefs, vol. 67, no. 9, pp. 1644-1648, Sep. 2020.

[6] Q. Deng, H. Sun, F. Chen, Y. Shu, H. Wang, and Y. Ha, "An optimized fpga-based real-time nift for 3d-lidar localization in smart vehicles," IEEE Transactions on Circuits and Systems II: Express Briefs, vol. 68, no. 9, pp. 3167-3171, Sep. 2021.

[7] E. Bank Tavakoli, A. Beygi, and X. Yao, "Rpkmn: An opencl-based fpga implementation of the dimensionality-reduced knn algorithm using random projection," IEEE Transactions on Very Large Scale Integration (VLSI) Systems, vol. 30, no. 4, pp. 549-552, April 2022.

[8] C. Wang, Z. Huang, A. Ren, and X. Zhang, "An fpga-based knn seach accelerator for point cloud registration," in 2024 IEEE International Symposium on Circuits and Systems (ISCAS), May 2024, pp. 1-5.

[9] F. Chen, R. Ying, J. Xue, F. Wen, and P. Liu, "Parallehn: A parallel octree-based nearest neighbor search accelerator for 3d point clouds," in 2023 IEEE International Symposium on High-Performance Computer Architecture (HPCA), Feb 2023, pp. 403-414.

[10] M. Han, L. Wang, L. Xiao, H. Zhang, T. Cai, J. Xu, Y. Wu, C. Zhang, and X. Xu, "Bitnn: A bit-serial accelerator for k-nearest neighbor search in point clouds," in 2024 ACM/IEEE 51st Annual International Symposium on Computer Architecture (ISCA), June 2024, pp. 1278-1292.

[11] F. Groh, L. Ruppert, P. Wieschollek, and H. P. A. Lensch, "Ggnn: Graphbased gpu nearest neighbor search," IEEE Transactions on Big Data, vol. 9, no. 1, pp. 267-279, Feb 2023.

[12] K. Koide, M. Yokozuka, S. Oishi, and A. Banno, "Voxelized gicp for fast and accurate 3d point cloud registration," in 2021 IEEE International Conference on Robotics and Automation (ICRA), May 2021, pp. 11 05411059.

[13] W. Dong, J. Park, Y. Yang, and M. Kaess, "Gpu accelerated robust scene reconstruction," in 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Nov 2019, pp. 7863-7870.

[14] R. Pinkham, S. Zeng, and Z. Zhang, "Quicknn: Memory and performance optimization of k-d tree based nearest neighbor search for 3d point clouds," in 2020 IEEE International Symposium on High Performance Computer Architecture (HPCA), Feb 2020, pp. 180-192.

[15] A. Kosuge, K. Yamamoto, Y. Akamine, and T. Oshima, "An soc-fpgabased iterative-closest-point accelerator enabling faster picking robots," IEEE Transactions on Industrial Electronics, vol. 68, no. 4, pp. 35673576, April 2021.

[16] T. Shan and B. Englot, "Lego-loam: Lightweight and ground-optimized lidar odometry and mapping on variable terrain," in 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Oct 2018, pp. 4758-4765.

[17] H. Wang, C. Wang, C.-L. Chen, and L. Xie, "F-loam: Fast lidar odometry and mapping," in 2021 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Sep. 2021, pp. 4390-4396.

[18] Y. Zhang, Z. Zhou, P. David, X. Yue, Z. Xi, B. Gong, and H. Forosoh, "Polarnet: An improved grid representation for online lidar point clouds semantic segmentation," in Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), June 2020, pp. $9601-9610$$9601-9610$ .

[19] R. Sun, J. Qian, R. H. Jose, Z. Gong, R. Miao, W. Xue, and P. Liu, "A flexible and efficient real-time orb-based full-hd image feature extraction accelerator," IEEE Transactions on Very Large Scale Integration (VLSI) Systems, vol. 28, no. 2, pp. 565-575, Feb 2020.

[20] R. Liu, J. Yang, Y. Chen, and W. Zhao, "eslam: An energy-efficient accelerator for real-time orb-slam on fpga platform," in 2019 56th ACM/IEEE Design Automation Conference (DAC), June 2019, pp. 16 .

[21] H. Yang, J. Shi, and L. Carlone, "Teaser: Fast and certifiable point cloud registration," IEEE Transactions on Robotics, vol. 37, no. 2, pp. 314333, April 2021.

[22] F. Ma, G. V. Cavalheiro, and S. Karaman, "Self-supervised sparse-to-dense: Self-supervised depth completion from lidar and monocular camera," in 2019 International Conference on Robotics and Automation (ICRA), May 2019, pp. 3288-3295.

[23] Y. Lyu, L. Bai, and X. Huang, "Chipnet: Real-time lidar processing for drivable region segmentation on an fpga," IEEE Transactions on Circuits and Systems I: Regular Papers, vol. 66, no. 5, pp. 1769-1779, May 2019.

[24] Y. Liu, J. Li, K. Huang, X. Li, X. Qi, L. Chang, Y. Long, and J. Zhou, "Mobilesp: An fpga-based real-time keypoint extraction hardware accelerator for mobile vslam," IEEE Transactions on Circuits and Systems I: Regular Papers, vol. 69, no. 12, pp. 4919-4929, Dec 2022.

[25] X. Zhang, L. Zhang, and X. Lou, "A raw image-based end-to-end object detection accelerator using bog features," IEEE Transactions on Circuits and Systems I: Regular Papers, vol. 69, no. 1, pp. 322-333, Jan 2022.

[26] Y. Li, M. Li, C. Chen, X. Zou, H. Shao, F. Tang, and K. Li, "Simdiff: Point cloud acceleration by utilizing spatial similarity and differential execution," IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, vol. 44, no. 2, pp. 568-581, Feb 2025.

[27] Y. Gao, C. Jiang, W. Piard, X. Chen, B. Patel, and H. Lam, "Hgpcn: A heterogeneous architecture for e2e embedded point cloud inference," in 2024 57th IEEE/ACM International Symposium on Microarchitecture (MICRO), Nov 2024, pp. 1588-1600.

[28] G. Yan, X. Liu, F. Chen, H. Wang, and Y. Ha, "Ultra-fast fpga implementation of graph cut algorithm with ripple push and early termination," IEEE Transactions on Circuits and Systems I: Regular Papers, vol. 69, no. 4, pp. 1532-1545, April 2022.

[29] C. Chen, X. Zou, H. Shao, Y. Li, and K. Li, "Point cloud acceleration by exploiting geometric similarity," in 2023 56th IEEE/ACM International Symposium on Microarchitecture (MICRO), Dec 2023, pp. 1135-1147.

[30] H. Sun, Q. Deng, X. Liu, Y. Shu, and Y. Ha, "An energy-efficient streambased fpga implementation of feature extraction algorithm for lidar point clouds with effective local-search," IEEE Transactions on Circuits and Systems I: Regular Papers, vol. 70, no. 1, pp. 253-265, Jan 2023.

[31] J. Xiao, H. Sun, Q. Deng, X. Liu, H. Zhang, C. He, Y. Shu, and Y. Ha, "Rps-km: An ultra-fast fpga accelerator of range-projection-structure k-nearest-neighbor search for lidar odometry in smart vehicles," in 2023 IEEE International Symposium on Circuits and Systems (ISCAS), May 2023, pp. 1-5.

[32] F. Chen, H. Yu, W. Jiang, and Y. Ha, "Quality optimization of adaptive applications via deep reinforcement learning in energy harvesting edge devices," IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, vol. 41, no. 11, pp. 4873-4886, Nov 2022.

[33] W. Jiang, H. Yu, H. Zhang, Y. Shu, R. Li, J. Chen, and Y. Ha, "Fodm: A framework for accurate online delay measurement supporting all timing paths in fpga," IEEE Transactions on Very Large Scale Integration (VLSI) Systems, vol. 30, no. 4, pp. 502-514, April 2022.